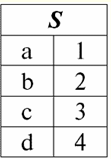
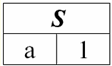
Aula No. 5. Álgebra Relacional. Operações Binárias

1. Operações de união, interseção, diferença

Quaisquer operações têm suas próprias regras de aplicabilidade que devem ser observadas para que expressões e ações não percam seu significado. As operações binárias da teoria dos conjuntos de união, interseção e diferença só podem ser aplicadas a duas relações necessariamente com o mesmo esquema de relação. O resultado de tais operações binárias serão relações constituídas por tuplas que satisfaçam as condições das operações, mas com o mesmo esquema de relação dos operandos.

1. O resultado operações sindicais duas relações r₁(S) e r₂(S) haverá uma nova relação r₃(S) consistindo dessas tuplas de relações r₁(S) e r₂(S) que pertencem a pelo menos uma das relações originais e com o mesmo esquema de relacionamento.

Assim, a intersecção das duas relações é:

r₃(S) = r₁(S) r₂(S) = {t(S) | t∈r₁ ∪t∈r₂};

Para maior clareza, aqui está um exemplo em termos de tabelas:

Sejam dadas duas relações:

r₁(S):

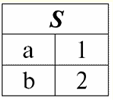
r₂(S):

Vemos que os esquemas da primeira e da segunda relações são os mesmos, só que possuem um número diferente de tuplas. A união dessas duas relações será a relação r₃(S), que corresponderá à tabela a seguir:

r3(S) = r₁(S) r₂(S):

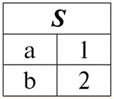
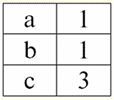
Assim, o esquema da relação S não mudou, apenas o número de tuplas aumentou.

2. Vamos passar para a consideração da próxima operação binária - operações de interseção dois relacionamentos. Como sabemos da geometria escolar, a relação resultante incluirá apenas as tuplas das relações originais que estão presentes simultaneamente em ambas as relações r₁(S) e r₂(S) (novamente, observe o mesmo padrão de relacionamento).

A operação de intersecção de duas relações ficará assim:

r₄(S) = r₁(S)∩r₂(S) = {t(S) | t ∈ r₁ & t ∈ r₂};

E novamente, considere o efeito desta operação nas relações apresentadas na forma de tabelas:

r₁(S):

r₂(S):

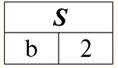
De acordo com a definição da operação pela intersecção das relações r₁(S) e r₂(S) haverá uma nova relação r₄(S), cuja visualização de tabela ficaria assim:

r₄(S) = r₁(S)∩r₂(S):

De fato, se olharmos para as tuplas da primeira e segunda relações iniciais, há apenas uma comum entre elas: {b, 2}. Tornou-se a única tupla da nova relação r₄(S).

3. Operação de diferença duas relações é definida de maneira semelhante às operações anteriores. As relações operando, como nas operações anteriores, devem ter os mesmos esquemas de relação, então a relação resultante incluirá todas aquelas tuplas da primeira relação que não estão na segunda, ou seja:

r₅(S) = r₁(S)\r₂(S) = {t(S) | t ∈ r₁ & t ∉ r₂};

As já conhecidas relações r₁(S) e r₂(S), em uma visualização tabular assim:

r₁(S):

r₂(S):

Consideraremos ambos os operandos na operação de intersecção de duas relações. Então, seguindo esta definição, a relação resultante r5(S) ficará assim:

r₅(S) = r₁(S)\r₂(S):

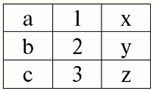
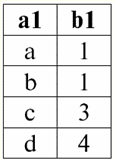
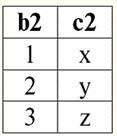
As operações binárias consideradas são básicas; outras operações, mais complexas, são baseadas nelas.

2. Produto cartesiano e operações de junção natural

A operação de produto cartesiano e a operação de junção natural são operações binárias do tipo produto e são baseadas na operação de união de duas relações que discutimos anteriormente.

Embora a ação da operação do produto cartesiano possa parecer familiar para muitos, vamos, no entanto, começar com a operação do produto natural, pois é um caso mais geral do que a primeira operação.

Portanto, considere a operação de junção natural. Deve-se notar imediatamente que os operandos desta ação podem ser relações com esquemas diferentes, em contraste com as três operações binárias de união, interseção e renomeação.

Se considerarmos duas relações com diferentes esquemas de relação r₁(S₁) e r₂(S₂), então seus composto natural haverá uma nova relação r₃(S₃), que consistirá apenas daquelas tuplas de operandos que combinam na interseção dos esquemas de relacionamento. Assim, o esquema do novo relacionamento será maior do que qualquer um dos esquemas de relações dos originais, pois é a conexão deles, "colando". A propósito, tuplas que são idênticas em duas relações de operandos, segundo as quais essa "colação" ocorre, são chamadas conectável.

Vamos escrever a definição da operação de junção natural na linguagem de fórmulas dos sistemas de gerenciamento de banco de dados:

r₃(S₃) = r₁(S₁)xr₂(S₂) = {t(S₁ ∪S₂) | t[S₁] ∈ r₁ &t(S₂) ∈ r₂};

Vamos considerar um exemplo que ilustra bem o trabalho de uma conexão natural, sua "cola". Sejam duas relações r₁(S₁) e r₂(S₂), na forma tabular de representação, respectivamente, iguais:

r₁(S₁):

r₂(S₂):

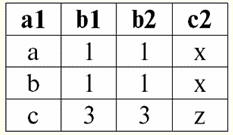
Vemos que essas relações têm tuplas que coincidem na interseção dos esquemas S₁ e S₂ relações. Vamos listá-los:

1) tupla {a, 1} da relação r₁(S₁) corresponde à tupla {1, x} da relação r₂(S₂);

2) tupla {b, 1} de r₁(S₁) também corresponde à tupla {1, x} de r₂(S₂);

3) a tupla {c, 3} corresponde à tupla {3, z}.

Assim, sob junção natural, a nova relação r₃(S₃) é obtido "colando" exatamente nessas tuplas. Então r₃(S₃) em uma visualização de tabela ficará assim:

r₃(S₃) = r₁(S₁)xr₂(S₂):

Acontece por definição: esquema S₃ não coincide com o esquema S₁, nem com o esquema S₂, "colamos" os dois esquemas originais cruzando as tuplas para obter sua junção natural.

Vamos mostrar esquematicamente como as tuplas são unidas ao aplicar a operação de junção natural.

Seja a relação r₁ tem uma forma condicional:

E a razão r₂ - Visão:

Então sua conexão natural ficaria assim:

Vemos que a "colagem" de operandos-relações ocorre de acordo com o mesmo esquema que demos anteriormente, considerando o exemplo.

Operação conexão cartesiana é um caso especial da operação de junção natural. Mais especificamente, ao considerar o efeito da operação do produto cartesiano nas relações, estipulamos deliberadamente que neste caso só podemos falar de esquemas de relações não-intersecionais. Como resultado da aplicação de ambas as operações, são obtidas relações com esquemas iguais à união de esquemas de relações de operandos, apenas todos os pares possíveis de suas tuplas caem no produto cartesiano de duas relações, pois os esquemas de operandos não devem em nenhum caso se cruzar.

Assim, com base no exposto, escrevemos uma fórmula matemática para a operação do produto cartesiano:

r₄(S₄) = r₁(S1)xr₂(S₂) = {t(S₁ ∪S₂) | t[S₁] ∈ r₁ &t(S₂) ∈ r₂}, S₁ ∩S₂= ∅;

Agora vamos ver um exemplo para mostrar como o esquema de relação resultante ficará ao aplicar a operação do produto cartesiano.

Sejam duas relações r₁(S1) e r₂(S₂), que são apresentados em forma de tabela da seguinte forma:

r₁(S₁):

r₂(S₂):

Então vemos que nenhuma das tuplas de relações r₁(S₁) e r₂(S₂), de fato, não coincide em sua intersecção. Portanto, na relação resultante r₄(S₄) todos os pares possíveis de tuplas das relações do primeiro e do segundo operando cairão. Pegue:

r₄(S₄) = r₁(S1)xr₂(S₂):

Obtivemos um novo esquema de relação r₄(S₄) não por "colar" tuplas como no caso anterior, mas pela enumeração de todos os diferentes pares de tuplas possíveis que não combinam na interseção dos esquemas originais.

Novamente, como no caso da junção natural, damos um exemplo esquemático da operação do produto cartesiano.

Deixe r₁ definido da seguinte forma:

E a razão r₂ dado:

Então seu produto cartesiano pode ser representado esquematicamente da seguinte forma:

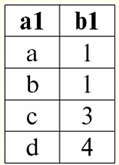
É assim que se obtém a relação resultante ao aplicar a operação do produto cartesiano.

3. Propriedades das operações binárias

Das definições acima das operações binárias de união, interseção, diferença, produto cartesiano e junção natural, seguem as propriedades.

1. A primeira propriedade, como no caso de operações unárias, ilustra relação de potência relações:

1) para a operação sindical:

|r₁ ∪r₂| ≤ |r₁| + |r₂|;

2) para a operação de interseção:

|r₁ ∩r₂ | ≤ min(|r₁|, |r₂|);

3) para a operação de diferença:

|r₁ \r₂| ≤ |r₁|;

4) para a operação do produto cartesiano:

|r₁ xr₂| = |r₁| |r₂|;

5) para operação de junção natural:

|r₁ xr₂| ≤ |r₁| |r₂|.

A razão de potências, como lembramos, caracteriza como o número de tuplas nas relações muda após a aplicação de uma ou outra operação. Então o que vemos? Poder associações duas relações r₁ e r₂ menor que a soma das cardinalidades dos operandos-relações originais. Por que isso está acontecendo? O problema é que, quando você mescla, as tuplas correspondentes desaparecem, sobrepondo-se umas às outras. Então, referindo-se ao exemplo que consideramos depois de passar por esta operação, você pode ver que na primeira relação havia duas tuplas, na segunda - três, e na resultante - quatro, ou seja, menos de cinco (a soma das cardinalidades das relações-operandos). Pela tupla correspondente {b, 2}, essas relações são "coladas".

Poder do resultado cruzamentos duas relações é menor ou igual à cardinalidade mínima das relações de operandos originais. Passemos à definição desta operação: apenas as tuplas que estão presentes em ambas as relações iniciais entram na relação resultante. Isso significa que a cardinalidade da nova relação não pode exceder a cardinalidade do operando-relação cujo número de tuplas é o menor dos dois. E a potência do resultado pode ser igual a essa cardinalidade mínima, pois o caso é sempre permitido quando todas as tuplas de uma relação de menor cardinalidade coincidem com algumas tuplas do segundo operando-relação.

Em caso de operação diferenças tudo é bastante trivial. De fato, se todas as tuplas que também estão presentes na segunda relação forem "subtraídas" do primeiro operando-relação, seu número (e, consequentemente, seu poder) diminuirá. Caso nenhuma tupla da primeira relação corresponda a qualquer tupla da segunda relação, ou seja, não há nada para "subtrair", seu poder não diminuirá.

Curiosamente, se a operação produto cartesiano a potência da relação resultante é exatamente igual ao produto das potências das duas relações de operandos. É claro que isso acontece porque todos os pares possíveis de tuplas das relações originais são escritos no resultado e nada é excluído.

E, finalmente, a operação conexão natural obtém-se uma relação cuja potência é maior ou igual ao produto das potências das duas relações originais. Novamente, isso acontece porque as relações de operandos são "coladas" por tuplas correspondentes, e as não correspondentes são excluídas completamente do resultado.

2. Propriedade de idempotência:

1) para a operação de união: r ∪ r = r;

2) para a operação de interseção: r ∩ r = r;

3) para a operação de diferença: r \ r ≠ r;

4) para a operação do produto cartesiano (no caso geral, a propriedade não é aplicável);

5) para a operação de junção natural: r x r = r.

Curiosamente, a propriedade da idempotência não é verdadeira para todas as operações acima, e para a operação do produto cartesiano, não é aplicável. De fato, se você combinar, cruzar ou conectar naturalmente qualquer relação consigo mesma, ela não mudará. Mas se você subtrair de uma relação exatamente igual a ela, o resultado será uma relação vazia.

3. Propriedade comutativa:

1) para a operação sindical:

r₁ ∪r₂ = r₂ ∪r₁;

2) para a operação de interseção:

r ∩ r = r ∩ r;

3) para a operação de diferença:

r₁ \r₂ ≠r₂ \r₁;

4) para a operação do produto cartesiano:

r₁ xr₂ = r₂ xr₁;

5) para operação de junção natural:

r₁ xr₂ = r₂ xr₁.

A propriedade de comutatividade vale para todas as operações, exceto para a operação de diferença. Isso é fácil de entender, pois sua composição (tuplas) não muda ao rearranjar as relações nos lugares. E ao aplicar a operação de diferença, é importante qual das relações de operandos vem primeiro, pois depende de quais tuplas de qual relação serão tomadas como referência, ou seja, com quais tuplas outras tuplas serão comparadas para exclusão.

4. Propriedade de associatividade:

1) para a operação sindical:

(r₁ ∪r₂) ∪r₃ = r₁ ∪(r₂ ∪r₃);

2) para a operação de interseção:

(r₁ ∩r₂)∩r₃ = r₁ ∩(r₂ ∩r₃);

3) para a operação de diferença:

(r₁ \r₂)\r₃ ≠r₁ \(r₂ \r₃);

4) para a operação do produto cartesiano:

(r₁ xr₂)xr₃ = r₁ x(r₂ xr₃);

5) para operação de junção natural:

(r₁ xr₂)xr₃ = r₁ x(r₂ xr₃).

E novamente vemos que a propriedade é executada para todas as operações, exceto para a operação de diferença. Isso é explicado da mesma forma que no caso da aplicação da propriedade de comutatividade. Em geral, as operações de união, interseção, diferença e junção natural não se importam com a ordem em que as relações dos operandos estão. Mas quando os relacionamentos são "tirados" um do outro, a ordem desempenha um papel dominante.

Com base nas propriedades e raciocínio acima, podemos tirar a seguinte conclusão: as três últimas propriedades, a saber, a propriedade de idempotência, comutatividade e associatividade, são verdadeiras para todas as operações que consideramos, exceto para a operação de diferença de duas relações , para o qual nenhuma das três propriedades indicadas foi satisfeita, e apenas em um caso a propriedade foi considerada inaplicável.

4. Opções de operação de conexão

Utilizando como base as operações unárias de seleção, projeção, renomeação e operações binárias de união, interseção, diferença, produto cartesiano e junção natural consideradas anteriormente (todas elas são geralmente chamadas de operações de conexão), podemos introduzir novas operações derivadas usando os conceitos e definições acima. Essa atividade é chamada de compilação. opções de operação de junção.

A primeira dessas variantes de operações de junção é a operação conexão interna de acordo com a condição de conexão especificada.

A operação de uma junção interna por alguma condição específica é definida como uma operação derivada do produto cartesiano e operações de seleção.

Escrevemos a definição da fórmula desta operação:

r₁(S₁)x _P r₂(S₂) = σ (r₁ xr₂),S₁ ∩S₂ =∅;

Aqui P = P<S₁ ∪S₂> - uma condição imposta à união de dois esquemas das relações-operandos originais. É por esta condição que as tuplas são selecionadas das relações r₁ e r₂ na relação resultante.

Observe que a operação de junção interna pode ser aplicada a relacionamentos com diferentes esquemas de relacionamento. Esses esquemas podem ser qualquer um, mas em nenhum caso eles devem se cruzar.

As tuplas das relações de operandos originais que são o resultado da operação de junção interna são chamadas tuplas juntáveis.

Para ilustrar visualmente a operação da operação de junção interna, daremos o exemplo a seguir.

Sejam dadas duas relações r₁(S₁) e r₂(S₂) com diferentes esquemas de relacionamento:

r₁(S₁):

r₂(S₂):

A tabela a seguir fornecerá o resultado da aplicação da operação de junção interna na condição P = (b1 = b2).

r₁(S₁)x _P r₂(S₂):

Assim, vemos que a "colagem" das duas tabelas que representam o relacionamento realmente aconteceu justamente para aquelas tuplas em que a condição da operação de junção interna P = (b1 = b2) é cumprida.

Agora, com base na operação de junção interna já apresentada, podemos introduzir a operação junção externa esquerda и junção externa direita. Vamos explicar.

O resultado da operação left outer join é o resultado da inner join, completado com tuplas não juntáveis ​​do operando-relação de origem esquerda. Da mesma forma, o resultado de uma operação de junção externa à direita é definido como o resultado de uma operação de junção interna, completada com tuplas não juntáveis ​​do operando de relação de origem destro.

A questão de como as relações resultantes das operações das junções externas esquerda e direita são reabastecidas é bastante esperada. Tuplas de um operando-relação são complementadas no esquema de outro operando-relação Valores nulos.

Vale a pena notar que as operações de junção externa esquerda e direita introduzidas dessa maneira são operações derivadas da operação de junção interna.

Para escrever as fórmulas gerais para as operações de junção externa esquerda e direita, realizaremos algumas construções adicionais.

Sejam dadas duas relações r₁(S₁) e r₂(S₂) com diferentes esquemas de relações S₁ e S₂, que não se cruzam.

Como já estipulamos que as operações de junção interna esquerda e direita são derivadas, podemos obter as seguintes fórmulas auxiliares para determinar a operação de junção externa esquerda:

1) r₃ (S₂ ∪S₁) ≔ r₁(S₁)x _Pr₂(S₂);

r ₃ (S₂ ∪S₁) é simplesmente o resultado da junção interna das relações r₁(S₁) e r₂(S₂). A junção externa esquerda é uma operação derivada da operação junção interna, e é por isso que começamos nossas construções com ela;

2) r₄(S₁) ≔ r ₃(S₂ ∪S₁) [S₁];

Assim, com a ajuda de uma operação de projeção unária, selecionamos todas as tuplas juntáveis ​​do operando-relação inicial esquerdo r₁(S₁). O resultado é designado r₄(S₁) para facilidade de uso;

3) r₅ (S₁) ≔ r₁(S₁)\r₄(S₁);

Aqui r₁(S₁) são todas as tuplas do operando de relação de origem à esquerda, e r₄(S₁) - suas próprias tuplas, apenas conectadas. Assim, usando a operação binária da diferença, em relação a r₅(S₁) obtivemos todas as tuplas não juntáveis ​​da relação do operando esquerdo;

4) r₆(S₂)≔{∅(S₂)};

{∅(S₂)} é uma nova relação com o esquema (S₂) contendo apenas uma tupla e composta por valores Null. Por conveniência, denotamos essa razão como r₆(S₂);

5) r₇ (S₂ ∪S₁) ≔ r₅(S₁)xr₆(S₂);

Aqui nós pegamos as tuplas não conectadas da relação operando à esquerda (r₅(S₁)) e os complementou no esquema do segundo operando de relação S₂ Valores nulos, ou seja, cartesiano multiplicado a relação consistindo dessas mesmas tuplas não juntáveis ​​pela relação r₆(S₂) definido no parágrafo quarto;

6) r₁(S1)→x _P r₂(S₂) ≔ (r₁ x _P r₂) ∪r₇ (S₂ ∪S₁);

Isto é junção externa esquerda, obtido, como pode ser visto, pela união do produto cartesiano dos operandos-relações originais r₁ e r₂ e relações r₇ (S₂ ∪ S₁) definido no parágrafo XNUMX.

Agora temos todos os cálculos necessários para determinar não apenas a operação da junção externa esquerda, mas por analogia e determinar a operação da junção externa direita. Então:

1) operação junção externa esquerda na forma estrita fica assim:

r₁(S₁) →x _P r₂(S₂) ≔ (r₁ x _P r₂) ∪ [(r₁ \(r₁ x _P r₂) [S₁]) x {∅(S₂)}];

2) operação junção externa direita é definido de maneira semelhante à operação left outer join e tem a seguinte forma:

r₁(S₁) →x _P r₂(S₂) ≔ (r₁ x _P r₂) ∪ [(r₂ \(r₁ x _P r₂) [S₂]) x {∅(S₁)}];

Essas duas operações derivadas têm apenas duas propriedades dignas de menção.

1. Propriedade da comutatividade:

1) para a operação de junção externa esquerda:

r₁(S₁) →x _P r₂(S₂) ≠ r₂(S₂) →x _P r₁(S₁);

2) para a operação de junção externa direita:

r₁(S₁) ←x _P r₂(S₂) ≠ r₂(S₂) ←x _P r₁(S₁)

Assim, vemos que a propriedade de comutatividade não é satisfeita para essas operações em termos gerais, mas as operações das junções externas esquerda e direita são mutuamente inversas, ou seja, o seguinte é verdadeiro:

1) para a operação de junção externa esquerda:

r₁(S₁) →x _P r₂(S₂) = r₂(S₂) →x _P r₁(S₁);

2) para a operação de junção externa direita:

r₁(S₁) ←x _P r₂(S₂) = r₂(S₂) ←x _Pr₁(S₁).

2. A principal propriedade das operações de junção externa esquerda e direita é que elas permitem restaurar o operando-relação inicial de acordo com o resultado final de uma determinada operação de junção, ou seja, são executados:

1) para a operação de junção externa esquerda:

r₁(S1) = (r₁ →x _P r₂) [S₁];

2) para a operação de junção externa direita:

r₂(S₂) = (r₁ ←x _P r₂) [S₂].

Assim, vemos que o primeiro operando-relação original pode ser restaurado a partir do resultado da operação de junção esquerda-direita, e mais especificamente, aplicando ao resultado desta junção (r₁ xr₂) a operação unária de projeção no esquema S₁,[S₁].

E da mesma forma, o segundo operando de relação original pode ser restaurado aplicando a junção externa direita (r₁ xr₂) a operação unária de projeção sobre o esquema da relação S₂.

Vamos dar um exemplo para uma consideração mais detalhada da operação das operações das junções externas esquerda e direita. Vamos introduzir as relações já familiares r₁(S₁) e r₂(S₂) com diferentes esquemas de relacionamento:

r₁(S₁):

r₂(S₂):

Tupla não juntável do operando de relação esquerdo r₂(S₂) é uma tupla {d, 4}. Seguindo a definição, são eles que devem complementar o resultado da conexão interna das duas relações de operandos originais.

Condição de junção interna das relações r₁(S₁) e r₂(S₂) também deixamos o mesmo: P = (b1 = b2). Então o resultado da operação junção externa esquerda haverá a seguinte tabela:

r₁(S₁) →x _P r₂(S₂):

De fato, como podemos ver, como resultado do impacto da operação de junção externa esquerda, o resultado da operação de junção interna foi reabastecido com tuplas não juntáveis ​​da esquerda, ou seja, no nosso caso, a primeira relação- operando. O reabastecimento da tupla no esquema do segundo operando de relação de origem (à direita), por definição, aconteceu com a ajuda de valores nulos.

E semelhante ao resultado junção externa direita pelo mesmo que antes, a condição P = (b1 = b2) das relações-operandos originais r₁(S₁) e r₂(S₂) é a seguinte tabela:

r₁(S₁) ←x _P r₂(S₂):

De fato, neste caso, o resultado da operação de junção interna deve ser reabastecido com tuplas não juntáveis ​​à direita, no nosso caso, o segundo operando-relação inicial. Tal tupla, como não é difícil ver, na segunda relação r₂(S₂) um, a saber {2, y}. Em seguida, atuamos na definição da operação da junção externa direita, complementando a tupla do primeiro operando (esquerdo) no esquema do primeiro operando com valores nulos.

Finalmente, vamos ver a terceira versão das operações de junção acima.

Operação de junção externa completa. Esta operação pode ser considerada não apenas como uma operação derivada de operações de junção interna, mas também como uma união de operações de junção externa esquerda e direita.

Operação de junção externa completa é definido como o resultado de completar a mesma junção interna (como no caso da definição de junções externas esquerda e direita) com tuplas não juntáveis ​​das relações de operandos iniciais esquerda e direita. Com base nesta definição, damos a forma de formulário desta definição:

r₁(S₁) ↔x _P r₂(S₂) = (r₁ →x _P r₂) ∪ (r₁ ←x _P r₂);

A operação de junção externa completa também tem uma propriedade semelhante à das operações de junção externa esquerda e direita. Somente devido à natureza recíproca original da operação de junção externa completa (afinal, ela foi definida como a união das operações de junção externa esquerda e direita), ela executa propriedade de comutatividade:

r₁(S₁) ↔x _P r₂(S₂)=r₂(S₂) ↔x _P r₁(S₁);

E para concluir a consideração das opções para operações de junção, vejamos um exemplo que ilustra a operação de uma operação de junção externa completa. Introduzimos duas relações r₁(S₁) e r₂(S₂) e a condição de junção.

Deixar

r₁(S₁)

r₂(S₂):

E deixe a condição de conexão das relações r₁(S₁) e r₂(S₂) será: P = (b1 = b2), como nos exemplos anteriores.

Então o resultado da operação full outer join das relações r₁(S₁) e r₂(S₂) pela condição P = (b1 = b2) teremos a seguinte tabela:

r₁(S₁) ↔x _P r₂(S₂):

Assim, vemos que a operação de junção externa completa justifica claramente sua definição como a união dos resultados das operações de junção externa esquerda e direita. A relação resultante da operação de junção interna é complementada por tuplas simultaneamente não juntáveis ​​como a esquerda (primeiro, r₁(S₁)) e à direita (segundo, r₂(S₂)) do operando de relação original.

5. Operações de derivativos

Assim, consideramos várias variantes de operações de junção, ou seja, as operações de junção interna, junção esquerda, direita e junção externa completa, que são derivadas das oito operações originais da álgebra relacional: operações unárias de seleção, projeção, renomeação e operações binárias de união, interseção, diferença, produto cartesiano e conexão natural. Mas mesmo entre essas operações originais há exemplos de operações com derivativos.

1. Por exemplo, operação cruzamentos duas razões é uma derivada da operação da diferença das mesmas duas razões. Vamos mostrar.

A operação de interseção pode ser expressa pela seguinte fórmula:

r₁(S)∩r₂(S) = r₁ \r₁ \r₂

ou, que dá o mesmo resultado:

r₁(S)∩r₂(S) = r₂ \r₂ \r₁;

2. Outro exemplo, a derivada da operação básica das oito operações originais é a operação conexão natural. Em sua forma mais geral, esta operação é derivada da operação binária do produto cartesiano e das operações unárias de selecionar, projetar e renomear atributos. Porém, por sua vez, a operação de junção interna é uma operação derivada da mesma operação do produto cartesiano de relações. Portanto, para mostrar que uma operação de junção natural é uma operação derivada, considere o exemplo a seguir.

Vamos comparar os exemplos anteriores para operações de junção natural e interna.

Sejam dadas duas relações r₁(S₁) e r₂(S₂) que atuarão como operandos. São iguais:

r₁(S₁):

r₂(S₂):

Como já recebemos anteriormente, o resultado da operação de junção natural dessas relações será uma tabela da seguinte forma:

r₃(S₃) ≔ r₁(S₁)xr₂(S₂):

E o resultado da junção interna das mesmas relações r₁(S₁) e r₂(S₂) pela condição P = (b1 = b2) teremos a seguinte tabela:

r₄(S₄) ≔ r₁(S₁)x _P r₂(S₂):

Vamos comparar esses dois resultados, as novas relações resultantes r₃(S₃) e r₄(S₄).

É claro que a operação de junção natural é expressa através da operação de junção interna, mas, mais importante, com uma condição de junção de uma forma especial.

Vamos escrever uma fórmula matemática que descreva a ação da operação de junção natural como uma derivada da operação de junção interna.

r₁(S₁)xr₂(S₂) = { ρ < ϕ₁>r₁ x _E ρ<ϕ₂>r₂}[S₁ ∪S₂],

onde E- condição de conectividade tuplas;

E= ∀a ∈S₁ ∩S₂ [IsNull(b1) & IsNull(2) ∪b1 = b2];

b₁ =ϕ₁ (nome(a)), b₂ =ϕ₂ (nomeia um));

Aqui está um dos renomear funções ϕ₁ é idêntico, e outra função de renomeação (ou seja, ϕ₂) renomeia os atributos onde nossos esquemas se cruzam.

A condição de conectividade E para tuplas é escrita de forma geral, levando em consideração as possíveis ocorrências de valores Null, pois a operação de junção interna (como mencionado acima) é uma operação derivada do produto cartesiano de duas relações e a operação de seleção unária.

6. Expressões de álgebra relacional

Vamos mostrar como as expressões e operações de álgebra relacional consideradas anteriormente podem ser usadas na operação prática de vários bancos de dados.

Vamos, por exemplo, termos à nossa disposição um fragmento de algum banco de dados comercial:

Fornecedores (Código de fornecedor, Nome do Fornecedor, Cidade do Fornecedor);

Ferramentas (Código da ferramenta, Nome da ferramenta,...);

Entregas (Código de fornecedor, código da peça);

Os nomes de atributos sublinhados[1] são atributos-chave (ou seja, identificadores), cada um em sua própria relação.

Suponha que nós, como desenvolvedores deste banco de dados e guardiões de informações sobre este assunto, sejamos obrigados a obter os nomes dos fornecedores (Nome do Fornecedor) e sua localização (Cidade do Fornecedor) no caso em que esses fornecedores não forneçam ferramentas com um nome genérico "Alicates".

Para determinar todos os fornecedores que atendem a esse requisito em nosso banco de dados possivelmente muito grande, escrevemos algumas expressões de álgebra relacional.

1. Formamos uma conexão natural das relações "Fornecedores" e "Suprimentos" para combinar com cada fornecedor os códigos das peças fornecidas por ele. A nova relação - resultado da aplicação da operação de junção natural - para conveniência de aplicação posterior, será denotada por r₁.

Fornecedores x Suprimentos ≔ r₁ (Código do Fornecedor, Nome do Fornecedor, Cidade do Fornecedor, Código de fornecedor, Código da ferramenta);

Entre parênteses, listamos todos os atributos das relações envolvidas nesta operação de junção natural. Podemos ver que o atributo "ID do fornecedor" está duplicado, mas no registro de resumo da transação, cada nome de atributo deve aparecer apenas uma vez, ou seja:

Fornecedores x Suprimentos ≔ r₁ (Código do fornecedor, nome do fornecedor, cidade do fornecedor, código do instrumento);

2. novamente formamos uma conexão natural, só que desta vez a relação obtida no parágrafo um e a relação Instrumentos. Fazemos isso para corresponder o nome desta ferramenta com cada código de ferramenta obtido no parágrafo anterior.

r₁ x Ferramentas [Código da ferramenta, Nome da ferramenta] ≔ r₂ (Código do Fornecedor, Nome do Fornecedor, Cidade do Fornecedor, Código da ferramenta, Código da ferramenta, Nome da ferramenta);

O resultado resultante será denotado por r₂, os atributos duplicados são excluídos:

r₁ x Ferramentas [Código da ferramenta, Nome da ferramenta] ≔ r₂ (Código do fornecedor, nome do fornecedor, cidade do fornecedor, código do instrumento, nome do instrumento);

Observe que tomamos apenas dois atributos da relação Tools: "Tool Code" e "Tool Name". Para fazer isso, nós, como pode ser visto a partir da notação da relação r₂, aplicou-se a operação de projeção unária: Ferramentas [código da ferramenta, nome da ferramenta], ou seja, se a relação Ferramentas fosse apresentada como uma tabela, o resultado desta operação de projeção seriam as duas primeiras colunas com os títulos "Código da ferramenta" e "Ferramenta nome" respectivamente ".

É interessante notar que os dois primeiros passos que já consideramos são bastante gerais, ou seja, podem ser usados ​​para implementar quaisquer outras requisições.

Mas os próximos dois pontos, por sua vez, representam passos concretos para alcançar a tarefa específica que temos diante de nós.

3. Escreva uma operação de seleção unária de acordo com a condição <"Nome da ferramenta" = "Alicate"> em relação à relação r₂obtido no parágrafo anterior. E nós, por sua vez, aplicamos a operação de projeção unária [Código do Fornecedor, Nome do Fornecedor, Cidade do Fornecedor] ao resultado dessa operação para obter todos os valores desses atributos, pois precisamos obter essas informações com base no ordem.

Assim:

(σ<Nome da ferramenta = "Alicates"> r₂) [Código do Fornecedor, Nome do Fornecedor, Cidade do Fornecedor] ≔ r₃ (Código do fornecedor, nome do fornecedor, cidade do fornecedor, código da ferramenta, nome da ferramenta).

Na razão resultante, denotada por r₃, apenas esses fornecedores (com todos os seus dados de identificação) acabaram por fornecer ferramentas com o nome genérico "Alicates". Mas em virtude do pedido, precisamos destacar aqueles fornecedores que, ao contrário, não fornecem tais ferramentas. Portanto, vamos passar para a próxima etapa do nosso algoritmo e escrever a última expressão da álgebra relacional, que nos dará a informação que estamos procurando.

4. Primeiro, vamos fazer a diferença entre a proporção "Fornecedores" e a proporção r₃, e após aplicar esta operação binária, aplicamos a operação de projeção unária nos atributos "Nome do Fornecedor" e "Cidade do Fornecedor".

(Fornecedores\r₃) [Nome do Fornecedor, Cidade do Fornecedor] ≔ r₄ (Código do fornecedor, nome do fornecedor, cidade do fornecedor);

O resultado é designado r₄, essa relação incluía apenas aquelas tuplas da relação "Fornecedores" original que correspondiam à condição do nosso pedido.

Assim, mostramos como, usando expressões e operações de álgebra relacional, você pode realizar todos os tipos de ações com bancos de dados arbitrários, realizar várias ordens, etc.

<< Voltar: Álgebra relacional. Operações unárias (Operação de seleção unária. Operação de projeção unária. Operação de renomeação unária. Propriedades das operações unárias)

>> Encaminhar: Linguagem SQL (O operador Select é o operador básico da linguagem de consulta estruturada. Operações unárias na linguagem de consulta estruturada. Operações binárias na linguagem de consulta estruturada. Operação de produto cartesiano. Operações de junção interna. Operação de junção natural. Operação de junção externa esquerda. Junção externa direita operação. Operação de junção externa completa)

Recomendamos artigos interessantes seção Notas de aula, folhas de dicas:

▪ Microeconomia. Berço

▪ Química orgânica. Berço

▪ Doenças cirúrgicas. Berço

Veja outros artigos seção Notas de aula, folhas de dicas.

Leia e escreva útil comentários sobre este artigo.

<< Voltar

Últimas notícias de ciência e tecnologia, nova eletrônica:

A existência de uma regra de entropia para o emaranhamento quântico foi comprovada 09.05.2024

A mecânica quântica continua a nos surpreender com seus fenômenos misteriosos e descobertas inesperadas. Recentemente, Bartosz Regula do Centro RIKEN de Computação Quântica e Ludovico Lamy da Universidade de Amsterdã apresentaram uma nova descoberta que diz respeito ao emaranhamento quântico e sua relação com a entropia. O emaranhamento quântico desempenha um papel importante na moderna ciência e tecnologia da informação quântica. No entanto, a complexidade da sua estrutura torna a sua compreensão e gestão um desafio. A descoberta de Regulus e Lamy mostra que o emaranhamento quântico segue uma regra de entropia semelhante à dos sistemas clássicos. Esta descoberta abre novas perspectivas na ciência e tecnologia da informação quântica, aprofundando a nossa compreensão do emaranhamento quântico e a sua ligação à termodinâmica. Os resultados do estudo indicam a possibilidade de reversibilidade das transformações de emaranhamento, o que poderia simplificar muito seu uso em diversas tecnologias quânticas. Abrindo uma nova regra ... >>

Mini ar condicionado Sony Reon Pocket 5 09.05.2024

O verão é uma época de relaxamento e viagens, mas muitas vezes o calor pode transformar essa época em um tormento insuportável. Conheça um novo produto da Sony – o minicondicionador Reon Pocket 5, que promete deixar o verão mais confortável para seus usuários. A Sony lançou um dispositivo exclusivo - o minicondicionador Reon Pocket 5, que fornece resfriamento corporal em dias quentes. Com ele, os usuários podem desfrutar do frescor a qualquer hora e em qualquer lugar, simplesmente usando-o no pescoço. Este miniar condicionado está equipado com ajuste automático dos modos de operação, além de sensores de temperatura e umidade. Graças a tecnologias inovadoras, o Reon Pocket 5 ajusta o seu funcionamento em função da atividade do utilizador e das condições ambientais. Os usuários podem ajustar facilmente a temperatura usando um aplicativo móvel dedicado conectado via Bluetooth. Além disso, camisetas e shorts especialmente desenhados estão disponíveis para maior comodidade, aos quais um mini ar condicionado pode ser acoplado. O dispositivo pode, oh ... >>

Energia do espaço para Starship 08.05.2024

A produção de energia solar no espaço está se tornando mais viável com o advento de novas tecnologias e o desenvolvimento de programas espaciais. O chefe da startup Virtus Solis compartilhou sua visão de usar a Starship da SpaceX para criar usinas orbitais capazes de abastecer a Terra. A startup Virtus Solis revelou um ambicioso projeto para criar usinas de energia orbitais usando a Starship da SpaceX. Esta ideia poderia mudar significativamente o campo da produção de energia solar, tornando-a mais acessível e barata. O cerne do plano da startup é reduzir o custo de lançamento de satélites ao espaço usando a Starship. Espera-se que este avanço tecnológico torne a produção de energia solar no espaço mais competitiva com as fontes de energia tradicionais. A Virtual Solis planeja construir grandes painéis fotovoltaicos em órbita, usando a Starship para entregar os equipamentos necessários. Contudo, um dos principais desafios ... >>

Notícias aleatórias do Arquivo Roteador de alta velocidade Asus RT-AC3200 28.07.2015 A Asus apresentou o roteador RT-AC3200. A novidade é equipada com seis antenas removíveis que suportam dois canais do padrão Wi-Fi 802.11ac (2,4 GHz / 5 GHz) - três antenas para transmissão e três antenas para recepção. Esta solução permitiu que os engenheiros da Asus alcançassem um desempenho incomparável até o momento, com uma taxa máxima de transferência de dados de 1300 Mbps (1,3 Gbps) em cada frequência na banda de 5 GHz. Com suporte para a tecnologia Broadcom TurboQAM, a taxa de transferência Wi-Fi 802.11n (2,4 GHz) aumenta de 450 Mbps para 600 Mbps para dispositivos compatíveis. Assim, teoricamente, a taxa de transferência de dados agregada do roteador pode ser de 3200 Mbps, o que, por exemplo, é 3 vezes maior que o padrão Gigabit Ethernet cabeado. Os engenheiros da Asus apontam especificamente que o roteador médio no mercado usando os antigos padrões Wi-Fi 802.11a/b/g pode diminuir a taxa de transferência de dados do padrão Wi-Fi 802.11ac mais rápido. O ASUS RT-AC3200, por sua vez, usa uma tecnologia Tri-Band Smart Connect de três bandas, que seleciona automaticamente um canal para cada dispositivo com base na velocidade de transmissão, intensidade do sinal e congestionamento sem intervenção do usuário. Dos recursos agradáveis, notamos a presença de uma chave de hardware no gabinete do dispositivo que desativa a operação dos LEDs - uma solução muito conveniente se o roteador estiver no seu quarto. O preço de varejo recomendado do Asus RT-AC3200 é 280 USD.

Outras notícias interessantes:

▪ A construção do palco principal do foguete superpesado Space Launch System é concluída

▪ Termômetro celular

▪ O mouse do computador pode digitar

▪ O laser coloca nanopontos

▪ Os cães também choram de alegria

Feed de notícias de ciência e tecnologia, nova eletrônica

Materiais interessantes da Biblioteca Técnica Gratuita:

▪ seção do site Carro. Seleção de artigos

▪ artigo Requisitos para iluminação de instalações e locais de trabalho. Noções básicas de uma vida segura

▪ artigo Como o príncipe russo Mstislav Vladimirovich se tornou o governante dos Kasogs? Resposta detalhada

▪ artigo Chefe do trem. Instrução padrão sobre proteção do trabalho

▪ artigo Desenhos duráveis ​​em compensado de madeira. Receitas e dicas simples

▪ artigo Conversor VHF. Enciclopédia de rádio eletrônica e engenharia elétrica

Deixe seu comentário neste artigo:

Todos os idiomas desta página

Arabic	Hebrew	Polish
Bengali	Hindi	Portuguese
Chinese	Italian	Spanish
English	Japanese	Turkish
French	Korean	Ukrainian
German	Malay	Vietnamese

Página principal | Biblioteca | Artigos | Mapa do Site | Revisões do site

www.diagrama.com.ua
2000-2024